Description

You are given two integer arrays nums1 and nums2. We write the integers of nums1 and nums2 (in the order they are given) on two separate horizontal lines.

We may draw connecting lines: a straight line connecting two numbers nums1[i] and nums2[j] such that:

• nums1[i] == nums2[j], and

• the line we draw does not intersect any other connecting (non-horizontal) line.

Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).

Return the maximum number of connecting lines we can draw in this way.

 

Example 1:

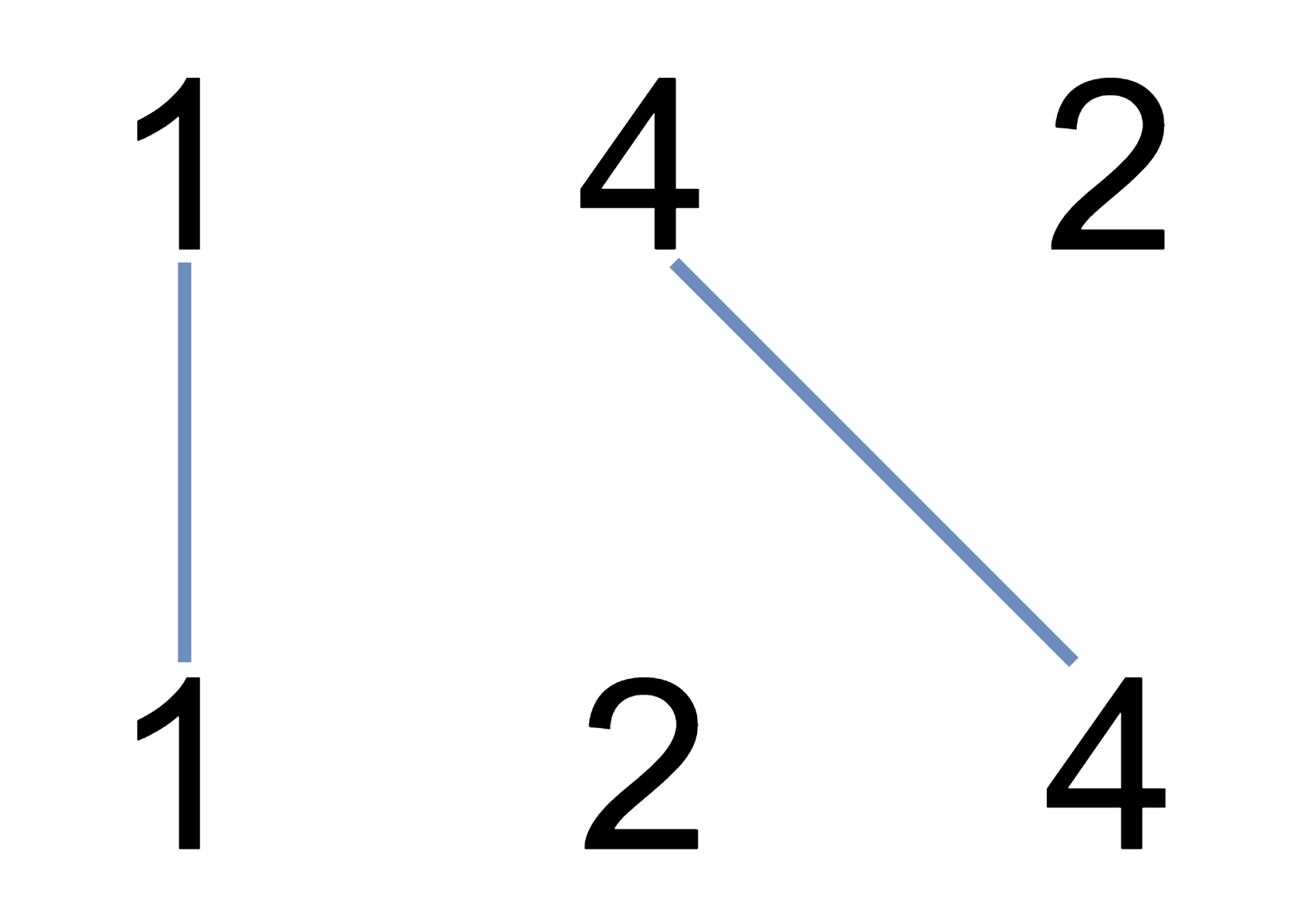
Input: nums1 = [1,4,2], nums2 = [1,2,4]

Output: 2 Explanation: We can draw 2 uncrossed lines as in the diagram. We cannot draw 3 uncrossed lines, because the line from nums1[1] = 4 to nums2[2] = 4 will intersect the line from nums1[2]=2 to nums2[1]=2.

 

Example 2:

Input: nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]

Output: 3

 

Example 3:

Input: nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]

Output: 2

 

Constraints:

• 1 <= nums1.length, nums2.length <= 500

• 1 <= nums1[i], nums2[j] <= 2000

Thinking

This is a typical dynamic programming problem, since it can be split into subproblems and solve respectively. Let's see the standard approach to the DP problem.

From my perspective, the hardest part of DP is to define the subproblem. As long as you find the transition, or say the way to split the problem, you can easily solve it. For this problem, let's define two cursor for nums1 and nums2, n1 and n2. Then For a problem solve(nums1, nums2, n1, n2) , if nums1[n1-1] == nums2[n2-1], the result is solve(nums1, nums2, n1-1, n2-1) + 1. Otherwise, the result is max(solve(nums1, nums2, n1-1, n2), solve(nums1, nums2, n1, n2-1)). Now, we have the big picture of the subproblem definition. Follow this definition, we will get the answer.

For DP problems, there are typically two ways to solve. First is the top-down approach, which is using the recursive function, we have a big problem, then we get its result from the lower layer, and recursively until we reach the bottom, just like from the top to go downward. Since it may involve repeat calculation, we usually add a memo to store the steps that we already calculated to optimize the speed. Second is the bottom-up approach, we get the result through the very basic blocks. For this problem, we can starting with n1=1 and n2=1, and accumulatively get the 'top layer' result, just like from the bottom to go upward.

Normally, we prefer the bottom-up approach (iteration) rather than the top-down approach (recursion) since the recursion may consume more resource and has lower efficiency. However, it is good to understand the top-down approach first because it is more in line with the human way of thinking。

Now, let's get to coding!

Top-down approach (Recursion)

​x
class Solution {
public:
    int recur(vector<int>& nums1, vector<int>& nums2, int n1, int n2, vector<vector<int>>& memo) {
        // Boundary check
        if(n1 == 0 || n2 == 0) return 0;
        
        // If we already calced it, just return
        if(memo[n1][n2] != -1) return memo[n1][n2];
        
        // Sub-problem logic
        if(nums1[n1-1] == nums2[n2-1]) {
            memo[n1][n2] = recur(nums1, nums2, n1-1, n2-1, memo) + 1;
        } else {
            memo[n1][n2] = max(recur(nums1, nums2, n1-1, n2, memo), recur(nums1, nums2, n1, n2-1, memo));
        }

        return memo[n1][n2];
    }

    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        int n1 = nums1.size(), n2 = nums2.size();

        vector<vector<int>> memo(n1+1, vector<int>(n2+1, -1));
        
        return recur(nums1, nums2, n1, n2, memo);
    }
};

Just like we discussed earlier, the parameter of the recursion function is defined exactly the same with the definition of the subproblem. Don't forget to check the boundary condition.

Bottom-up approach

xxxxxxxxxx
class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        int n1 = nums1.size(), n2 = nums2.size();
        vector<vector<int>> dp(n1+1, vector<int>(n2+1, 0));

        for(int i=1;i<=n1;++i) {
            for(int j=1;j<=n2;++j) {
                if(nums1[i-1] == nums2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
                else {
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
                }
            }
        }

        return dp[n1][n2];
    }
};

The dp vector is basically the same as the memo, only this time we calculate its value from the bottom, i.e. n1=1 and n2=1.

Bottom-up with space optimization

If we see i as the round, noticing that each round dp[i][j] only associate with either this round dp[i][x] or the last round dp[i-1][x]. Therefore, we can optimize the space of dp from i to 2, that is dp[2][n2]. The transition is also straight forward. Let dp[0] denote the last round which is i-1 and dp[1]denote the current round which is i. thus, we can substitute all i-1to 0 and i to 1, and at the end of each round refresh the 'last round' dp[0], then we get the final result. Here is the code:

xxxxxxxxxx
class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        int n1 = nums1.size(), n2 = nums2.size();
        
        // Optimize space compexity to O(min(n1, n2))
        if(n1 < n2) return maxUncrossedLines(nums2, nums1);
        
        vector<vector<int>> dp(2, vector<int>(n2+1, 0));

        for(int i=1;i<=n1;++i) {
            for(int j=1;j<=n2;++j) {
                if(nums1[i-1] == nums2[j-1]) dp[1][j] = dp[0][j-1] + 1;
                else {
                    dp[1][j] = max(dp[0][j], dp[1][j-1]);
                }
            }
            dp[0] = dp[1];
        }

        return dp[0][n2];
    }
};

What I learned

Dynamic programming is a type of relatively hard problem. This is a good practice for my old knowledge. Thanks to the class EE538 in USC, it was very enlightening for me to understand the ideology of dynamic programming. Fight on!