2023-05-10 LeetCode Daily Problem 59. Spiral Matrix
Description
Given a positive integer
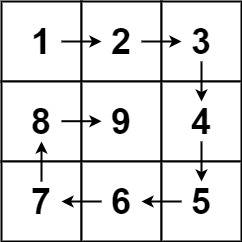
n, generate annxnmatrix filled with elements from1ton^2in spiral order.Example 1:
Input:n = 3
Output:[[1,2,3],[8,9,4],[7,6,5]]Example 2:
Input:n = 1
Output:[[1]]
My Orignal Approach
It is pretty much a simulation for this process. We can view a 360 degree process as a round, and that we get a while loop.
We maintain two variable row and column. Each round, we traverse a row in ascending order, a column in ascending order, then another row in descending order, finally a column in descending order.
// My original code, O(n^2) time complexity
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
int row = n, column = n, curr = 1, i = 0, j = 0;
vector<vector<int>> ans(n, vector<int>(n));
while(row > 0 && column > 0) {
// Ascending row
int row_tmp = row;
while(row_tmp > 0) {
ans[i][j++] = curr++;
row_tmp--;
}
i += 1;
j -= 1;
column -= 1;
// Ascending column
int column_tmp = column;
while(column_tmp > 0) {
ans[i++][j] = curr++;
column_tmp--;
}
j -= 1;
i -= 1;
row -= 1;
// Descending row
row_tmp = row;
while(row_tmp > 0) {
ans[i][j--] = curr++;
row_tmp--;
}
j += 1;
i -= 1;
column -= 1;
// Descending column
column_tmp = column;
while(column_tmp > 0) {
ans[i--][j] = curr++;
column_tmp--;
}
i += 1;
j += 1;
row -= 1;
}
return ans;
}
};Not so sloppy Approach
Following the editorial, I optimized my code to a more general and readable one. We can abstract each round as a `layer`, and all the directional process is related to `n` and `layer`. The relationship is shown in below.

So just need to handle the relationship of `layer` and `n` to abstract a general ’round’. Here is the code.
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
int row = n, column = n, curr = 1, i = 0, j = 0;
vector<vector<int>> ans(n, vector<int>(n));
for(int layer = 0; layer < (n+1) / 2; layer++) {
for(int row_tmp = layer; row_tmp < n - layer; ++row_tmp) {
ans[layer][row_tmp] = curr++;
}
for(int column_tmp = layer + 1; column_tmp < n - layer; ++column_tmp) {
ans[column_tmp][n - layer - 1] = curr++;
}
for(int row_tmp = n - layer - 2; row_tmp >= layer; row_tmp--) {
ans[n - layer - 1][row_tmp] = curr++;
}
for(int column_tmp = n - layer - 2; column_tmp > layer; column_tmp--) {
ans[column_tmp][layer] = curr++;
}
}
return ans;
}
};Last but not least – Optimized approach
This method is learned from the editorial, but not so easy to come up with in a short time.
Please see details in the code comment.
// O(n^2) time complexity
class Solution {
public:
// This function can output a non-negative mod of x % y
int floorMod(int x, int y) {
return ((x % y) + y) % y;
}
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> result (n, vector<int>(n, 0));
int cnt = 1; // The answer counter
// {row ascending, col ascending, row descending, col descending}
int dir[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
int d = 0; // Direction
int row = 0;
int col = 0;
while (cnt <= n * n) {
result[row][col] = cnt++;
// r, c refers to the next point
int r = floorMod(row + dir[d][0], n);
int c = floorMod(col + dir[d][1], n);
// change direction if next cell is non zero
// *when this direction reaches the end, the result[r][c] will be reset
// to the starting point of the iteration of this direction which is
// clearly not 0 (the default empty value), that means the direction need to change.
if (result[r][c] != 0) d = (d + 1) % 4;
row += dir[d][0];
col += dir[d][1];
}
return result;
}
};What I learned
- For the original approach, I thought the non-positive value would be
false, yet it is not true, I mean literally, not true. Only0value will be seen asfalse. This detail though subtle, I’m still feeling good to know about it as early as possible. - The direction method is cool, as well as that
floorModmethod. Maybe we can thinking about the mindset of this approach.