Given a directed acyclic graph, with n vertices numbered from 0 to n-1, and an array edges where edges[i] = [fromi, toi] represents a directed edge from node fromi to node toi.
Find the smallest set of vertices from which all nodes in the graph are reachable. It's guaranteed that a unique solution exists.
Notice that you can return the vertices in any order.
Example 1:
Input:
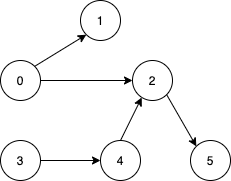
n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]Output:
[0,3]Explanation: It's not possible to reach all the nodes from a single vertex. From 0 we can reach [0,1,2,5]. From 3 we can reach [3,4,2,5]. So we output [0,3].
Example 2:
Input:
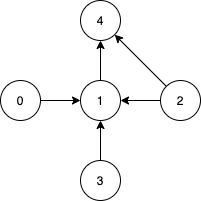
n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]Output:
[0,2,3]Explanation: Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.
Constraints:
2 <= n <= 10^5
1 <= edges.length <= min(10^5, n * (n - 1) / 2)
edges[i].length == 2
0 <= fromi, toi < nAll pairs
(from_i, to_i)are distinct.
Thinking
Initially, I was thinking about using Union Set/Find, since we can use it to trace to the root and get one of the result. But then I realized that if one node has two indegree, the union set will get confused 🤣 Then! As my mind goes the the indegree, and this question is about DAG (Directed Acyclic Graph), I began to evaluate the possibility with topological sort. The topological sort is basically all about the indegree and outdegree. In this problem, we can find that all the result nodes has no indegree and only has outdegree.
Solution
For this problem, the node tag is always from 0 to n-1, so we can use vector to markup the indegree information instead of set or map.
xclass Solution {public: vector<int> findSmallestSetOfVertices(int n, vector<vector<int>>& edges) { vector<int> marker(n, 1);
for(auto& edge : edges) { marker[edge[1]] = 0; }
vector<int> ans; ans.reserve(n);
for(int i=0; i<n; ++i) { if(marker[i]) { ans.push_back(i); } }
return ans; }};What I learned
DAG problems <—–> Topological sort